问题描述#

给定一个集合 $A=\{a_1,a_2,a_3,\cdots,a_n\}$ ，以及集合 $A$ 上的关系 $R=\{(a_i,a_j)a_i、a_j\in A,i\neq j\}$ ，其中 $(a_i,a_j)$ 表示 $a_i$ 与 $a_j$ 之间的冲突关系。现要将 $A$ 划分为若干个子集，要求子集中所有元素均无冲突，且划分的子集尽可能少。

举个简单的例子：假设运动会设立了 9 个比赛项目，则 $A=\{1,2,3,4,5,6,7,8,9\}$ 。其中项目的冲突情况如下：

R=\{(2,8),(9,4),(2,9),(2,1),(2,5),(6,2),(5,9),(5,6),(5,4),(7,5),(7,6),(3,7),(6,3)\}

现在要做的就是将项目集合 $A$ 划分成若干个子集，使同个子集中各项目不发生冲突。

算法分析#

前置变量#

首先，我们可以将关系集合 $R$ 转化成一个 n 阶矩阵 R[n][n]，如果 $a_i$ 与 $a_j$ 冲突，则 $R[i][j]=R[j][i]=1$ ，否则为 $0$ ：

冲突矩阵

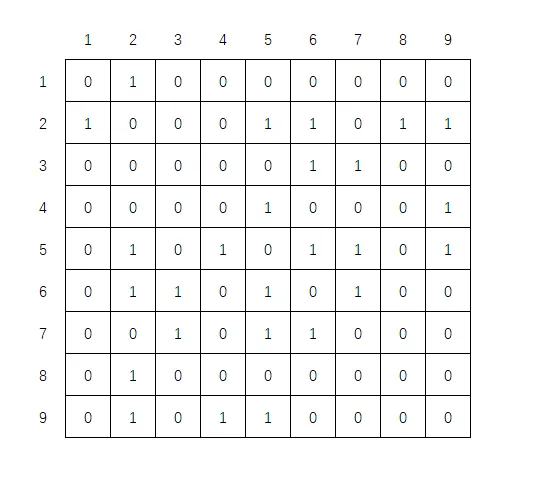
定义一个循环队列 cq[n]，用来存储当前还未被分组的元素；

定义一个数组 result[n]，用来存储每个项目的分组信息；

定义一个数组 newr[n]，用来存储当前分组的冲突信息。

算法逻辑#

将集合 $A$ 中的元素放入 cq 中，result 所有值置为 0，newr 所有值置为 0。即：

										front, rear
										↓
		0	1	2	3	4	5	6	7	8
-------------------------------------------
cq:		1	2	3	4	5	6	7	8	9	
newr:	0	0	0	0	0	0	0	0	0
result:	0	0	0	0	0	0	0	0	0

设置分组为 1，即 group = 1。设置 front = (front + 1)%n，即将对头指向 cq 第一个元素，从第一个元素开始，执行以下操作：

cq 第一个元素出队（front 所指的元素出队），将这个元素在 $R$ 中的对应行加到 newr 数组中，设置 result[0] = 1；
NOTE
因为初始时已经将 front 指向了第一个元素，所以出队后 front 要后移，就指到第二个元素了。
```
			front						rear
			↓							↓
		0	1	2	3	4	5	6	7	8	
-------------------------------------------
cq:			2	3	4	5	6	7	8	9
newr:	0	1	0	0	0	0	0	0	0	
result:	1	0	0	0	0	0	0	0	0	
```

检查第二个元素，先将其出队，因为第二个元素与第一个元素有冲突（newr[1] == 1），再将其入队；

		rear	front
		↓		↓
		0	1	2	3	4	5	6	7	8
-------------------------------------------
cq:		2		3	4	5	6	7	8	9	
newr:	0	1	0	0	0	0	0	0	0
result:	1	0	0	0	0	0	0	0	0

检查第三个元素，先将其出队，第三个元素与第一个元素无冲突，将 R 的对应行加到 newr 上，出队并设置 result[2] = 1；
NOTE
这里将 R 对应的行加到 newr 上的目的是为了方便判断新的元素是否与之前的元素冲突。
例如 1 元素与 2 元素冲突，2 元素与 5 元素冲突。如果只把 newr 设置为 R 第一行的话，就无法通过 newr 检测 5 元素的冲突关系，而在检测出 2 元素冲突后将 R 的第二行加到 newr 上的话，就相当于把 2 元素的冲突关系加到 newr 数组中，就可以直接判断其他元素的冲突关系了。
```
		rear		front
		↓			↓
		0	1	2	3	4	5	6	7	8
-------------------------------------------
cq:		2			4	5	6	7	8	9	
newr:	0	1	0	0	0	1	1	0	0
result:	1	0	1	0	0	0	0	0	0
```

检查第四个元素，先将其出队，它与第一、三个元素均无冲突，将 R 的对应行加到 newr 上，出队并设置 result[3] = 1；

		rear			front
		↓				↓
		0	1	2	3	4	5	6	7	8
-------------------------------------------
cq:		2				5	6	7	8	9	
newr:	0	1	0	0	1	1	1	0	1
result:	1	0	1	1	0	0	0	0	0

检查第五、六、七个元素，先将其出队，它们与第一、三、四个元素冲突（即 newr[4] == 1，newr[5] == 1，newr[6] == 1），再将其入队；

					rear			front
					↓				↓
		0	1	2	3	4	5	6	7	8
-------------------------------------------
cq:		2	5	6	7				8	9	
newr:	0	1	0	0	1	1	1	0	1
result:	1	0	1	1	0	0	0	0	0

检查第八个元素，先将其出队，它与第一、三、四个元素均无冲突，将 R 的对应行加到 newr 上，出队并设置 result[7] = 1；

					rear				front
					↓					↓
		0	1	2	3	4	5	6	7	8
-------------------------------------------
cq:		2	5	6	7					9	
newr:	0	2	0	0	1	1	1	0	1
result:	1	0	1	1	0	0	0	1	0

检查第九个元素，先将其出队，它与第一、三、四、八个元素冲突，再将其入队；

		front			rear
		↓				↓
		0	1	2	3	4	5	6	7	8
-------------------------------------------
cq:		2	5	6	7	9				
newr:	0	2	0	0	1	1	1	0	1
result:	1	0	1	1	0	0	0	1	0

这样就完成了一轮筛选，根据 result 数组我们可以看出 $a_1,a_3,a_4,a_8$ 四个元素被分到了第 1 组。我们将 group 值加 1，然后再按以上步骤遍历 cq 队列，直到 cq 为空，就将所有元素划分完毕了。

算法实现#

void DivideIntoGroup(int n, int R[][n], int cq[], int result[]) {
    /*
    * @param `n`: 集合 A 的元素个数
    * @param `R`: 集合 A 的冲突矩阵
    * @param `cq`: 存储当前仍未被分组的元素
    * @param `result`: 存储分组结果
    */
    int front, rear, group, pre, I, i; // I 是为了可读性，手动将数组下标加 1 赋给 I
    front = n - 1;
    rear = n - 1; // 将头尾指针均指向最后一个元素
    for (i = 0; i < n; i++) {
        newr[i] = 0;
        cq[i] = i + 1;
    }
    group = 1; // 以上为初始化过程
    
    pre = 0; // 前一个出队元素的编号
    do {
        front = (front + 1)%n; // 将队头指针指向下一个元素，也就是出队操作（出队的那个元素从逻辑上删除而非物理上删除）
        I = cq[i];
        if (I < pre) { // 正常按顺序从第一个元素到最后一个元素遍历的情况下，I 应该是逐项增大的，如果 I < pre，说明循环队列已经循环了一个周期了，直接进行下一次筛选
            group = group + 1;
            result[I - 1] = group;
            for (i = 0; i < n; i++) {
                newr[i] = R[I - 1][i];
            }
        } else if (newr[I - 1] != 0) { // 发生冲突，则需要将其重新入队
            rear = (rear + 1)%n;
            cq[rear] = I;
        } else { // 不发生冲突，归入到同一组
            result[I - 1] = group;
            for (i = 0; i < n; i++) { // 把当前元素在 R 中对应的行加到 newr 上
                newr[i] = newr[i] + R[I - 1][i];
            }
        }
        pre = I;
    } while(rear != front);
}